What is ABC?
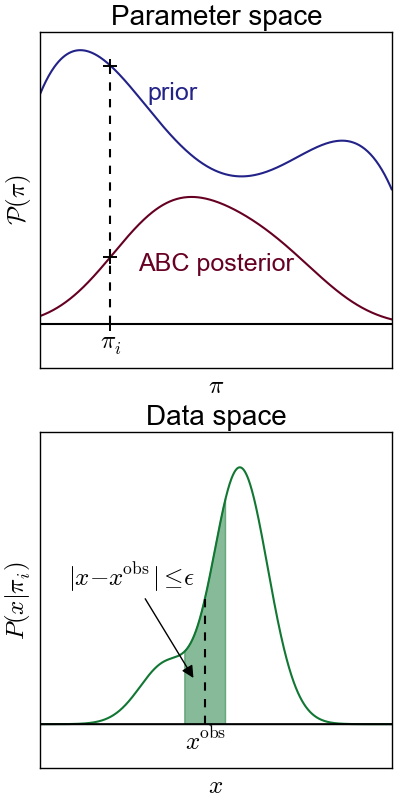
Approximate Bayesian computation (ABC) is a powerful parameter inference method using an accept-reject process which bypasses smartly the likelihood evaluation. To apply ABC, the model needs to be stochastic. It also requires the choice of a distance $|x-y|$ and a tolerance level $\epsilon$.
How does ABC work?
Given an observation $x^\mathrm{obs}$, the ABC algorithm processes the following steps:
- Draw a parameter $\pi$ from the prior
- Draw a $x$ from the model $P(\cdot|\pi)$
- Accept $\pi$ if $|x - x^\mathrm{obs}|\leq\epsilon$
- Reject otherwise
- Repeat and reconstruct the distribution of accepted $\pi$
Why does this work? Because \[ \definecolor{LincBlue}{RGB}{34,34,136} \definecolor{LincDarkRed}{RGB}{102,0,34} \definecolor{LincGreen}{RGB}{17,119,51} \textcolor{LincDarkRed}{\mathrm{Distribution\ of\ accepted }\ \pi}\ \ \ \ \ \ \ \ \ \ \ \\ =\ \textcolor{LincBlue}{\mathrm{prior}}\ \times\ \textcolor{LincGreen}{\mathrm{green\ areas}}\\ \ \ \ \ \ \ \ \approx\ \textcolor{LincBlue}{\mathrm{prior}}\ \times\ 2\epsilon\ \times\ \mathrm{likelihood}\\ \propto\ \mathrm{posterior}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \] Therefore, ABC is actually a sampling from the posterior. We only need to reconstruct the distribution of accepted $\pi$ to recover it.
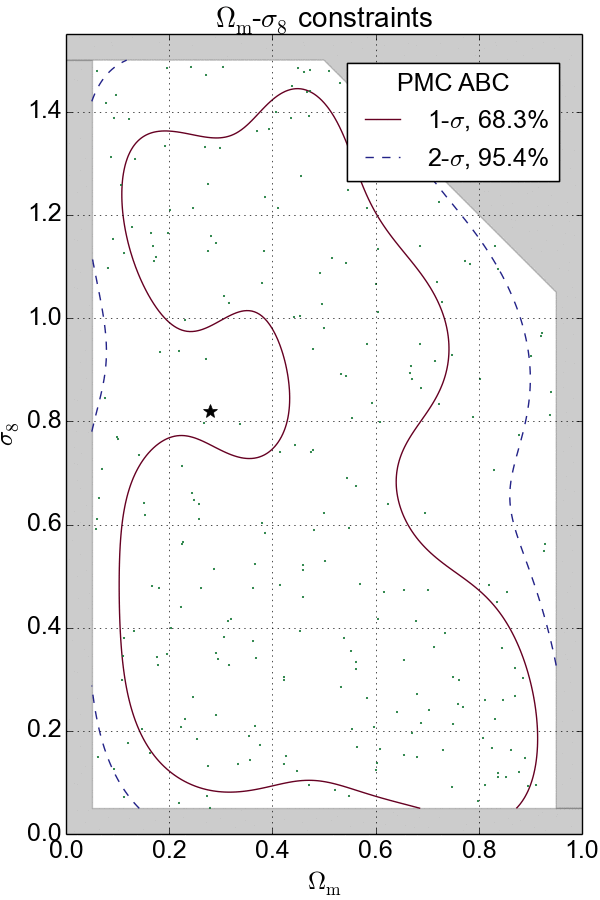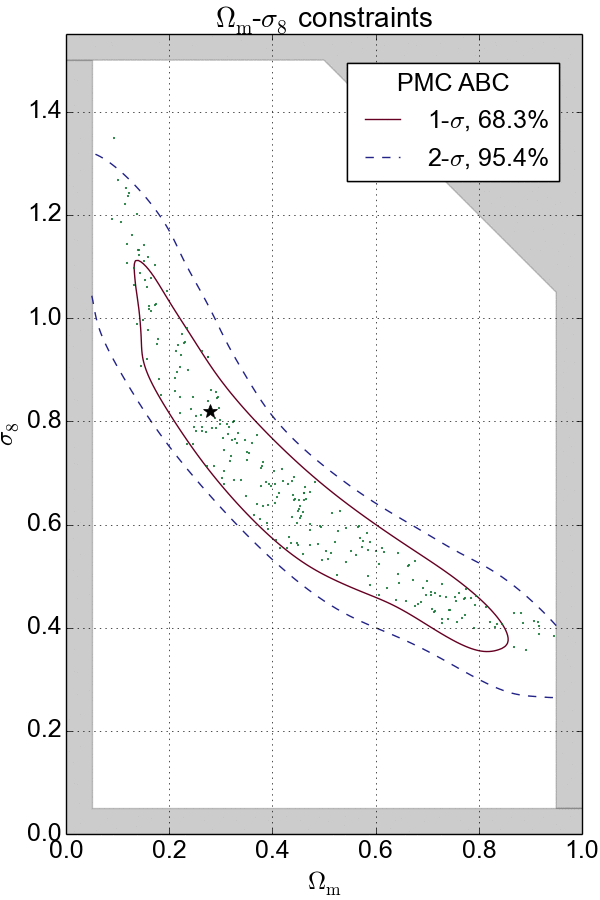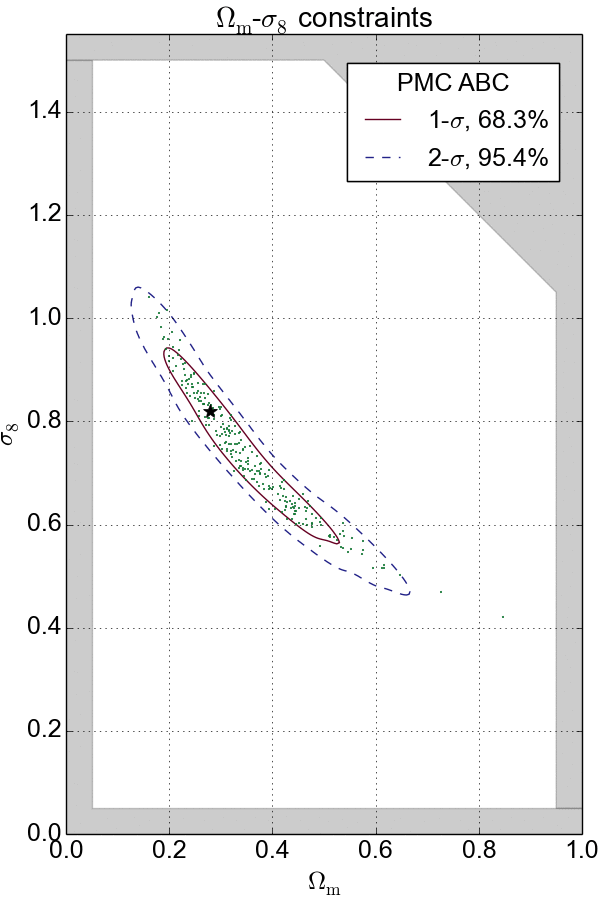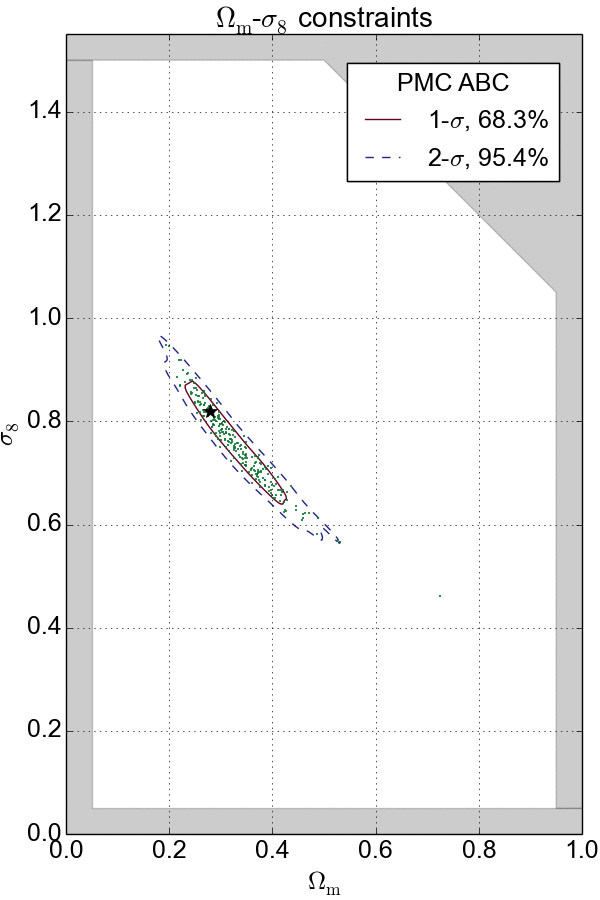
Combination with PMC
If $\epsilon$ is too large, the approximation is bad; if $\epsilon$ is too small, then the sampling will be inefficient. To solve this problem, ABC is often combined with the population Monte Carlo (PMC) technique, an iterative solution for the choice of $\epsilon$. PMC ABC decreases $\epsilon$ gradually to converge the constraints.